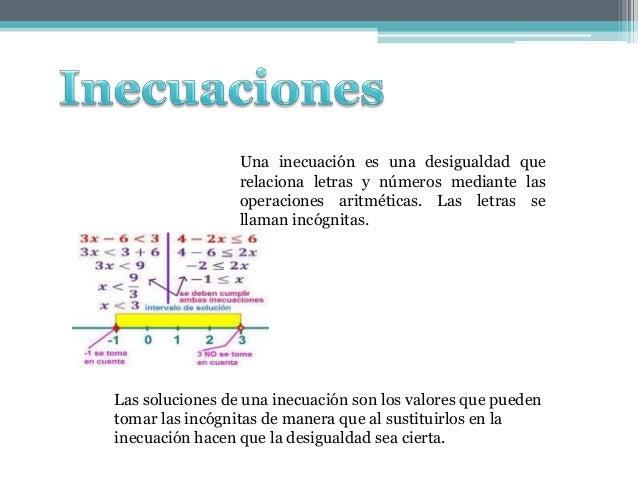
Inecuación

Del mismo modo en qué se hace la diferencia de igualdad y ecuación, una inecuación que es válida para todas las variables se llama inecuación incondicional y las qué son válidas sólo para algunos valores de las variables se conocen cómo inecuaciones condicionales.¹​ Los valores que verifican la desigualdad, son sus soluciones.

• Ejemplo de inecuación incondicional: ${\displaystyle |x|\leq |x|+|y|}$.
• Ejemplo de inecuación condicional: ${\displaystyle -2x+7<2}$.

Clasificación[editar]

Los criterios más comunes de clasificación del ejemplo: ${\displaystyle x<0}$.

• • De dos incógnitas. Ejemplo: ${\displaystyle x<y}$.
  • De tres incógnitas. Ejemplo: ${\displaystyle x<y+z}$.
  • etc.

• Según la potencia de la incógnita,
  • De primer grado o lineal. Cuando el mayor exponente de la incógnita de la inecuación es uno. Ejemplo: ${\displaystyle x+1<0}$.
  • De segundo grado o cuadrática. Cuando el mayor exponente de cualquiera de sus incógnitas es dos. Ejemplo: ${\displaystyle x^{2}+1<0}$.
  • De tercer grado o cúbica. Cuando el mayor exponente de cualquiera de sus incógnitas es tres. Ejemplo: ${\displaystyle x^{3}+y^{2}<0}$.
  • etc.

Nota: estas clasificaciones no son mutuamente excluyentes, como se muestra en el último ejemplo.

Inecuaciones de segundo grado con una incógnita[editar]

Se expresan a través de cualquiera de las desigualdades siguientes (con a, b y c números reales, y a distinto de cero):

• ${\displaystyle ax^{2}+bx+c<0}$
• ${\displaystyle ax^{2}+bx+c\leq 0}$
• ${\displaystyle ax^{2}+bx+c>0}$
• ${\displaystyle ax^{2}+bx+c\geq 0}$
• a = 0

Sistema de Inecuaciones[editar]

Véase también: Programación lineal

La región de viabilidad en un problema de programación lineal está definida por un sistema de inecuaciones.

En un sistema de inecuaciones intervienen dos o más inecuaciones. No todos los sistemas de inecuaciones tienen solución.

Sistema de inecuaciones de primer grado con una incógnita[editar]

Es un conjunto de inecuaciones de primer grado

${\displaystyle \left\{{\begin{array}{rcrcrcr}ax+b<0\\cx+d\geq 0\\...\\lx+m>0\\\end{array}}\right.}$ ||left}}

La solución del sistema será el conjunto de números reales que verifican a la vez todas las inecuaciones.

INECUACCIONES CUADRITIVAS

Inecuaciones cuadráticas. Inecuaciones cuadráticas o de segundo grado son desigualdades donde la variable de mayor exponente tiene grado dos (2).

Contenido

 [ocultar] 

• 1 Definición
• 2 Ejemplo de inecuación cuadrática
• 3 Sugerencias para resolver inecuaciones cuadráticas
• 4 Ejemplo resuelto
• 5 Ejercicios propuestos
• 6 Fuentes
• 7 Enlaces externos

Definición

Una inecuación cuadrática o de segundo grado es una desigualdad donde la variable tiene exponente 2 y es en su forma general de una de las formas siguientes ax2 + bx + c ≥ 0, ax2 + bx + c ≤ 0, ax2 + bx + c > 0 ó ax2 + bx + c ; 0, también puede tener el signo de desigualdad (d≥ bx + c), pero se puede llevar a una de las formas anteriores haciendo transformaciones equivalentes.

Ejemplo de inecuación cuadrática

x2 + 2x < 15 y 4x2 ≥ 12x -9

Sugerencias para resolver inecuaciones cuadráticas

1. Escribe la inecuación en su forma general, es decir comparada con cero.
2. Halla los ceros de la ecuación cuadrática ax2 + bx + c = 0  (Por Descomposición en factores o por la fórmula del discriminante). Si el Discriminante es menor que cero la solución es todos los reales o no tiene solución, dependiendo de la desigualdad y del signo de ¨a¨.
3. Representa esos ceros en una Recta numérica.
4. Analiza el signo de ese Trinomio en los Intervalos determinados por los ceros,  evaluando el Polinomio en valores cómodos de esos intervalos o ubicando los signos de derecha a izquierda (Si a>0 comienza con el signo más y alternando menos y luego más, si a < 0 comienza con menos y de igual forma alterna, el siguiente gráfico hace referencia en caso de ¨ a ¨ positivo).
5. Escribe la solución en notación de intervalo, teniendo en cuenta que si la desigualdad es estricta los ceros no se incluyen y en caso contrario se incluyen en la solución.

Nota importante: Después de comparar con cero se obtiene una Función cuadrática y por eso es que se buscan sus ceros y se hace el análisis de los signos de dicha función en esos Intervalos, ya que la función cuadrática representa una Parábola que puede abrir hacia arriba o hacia abajo según el signo de a. Gráfico de una parábola

Ejemplo resuelto

Halla la solución de la siguiente inecuación cuadrática.

1) x2 – 2x > 3

Respuesta.

1. x2 – 2x – 3 > 0

x2 – 2x – 3 = 0

(x – 3) (x+1) = 0 x = -1 ó x = 3

Rta. x Real: x > 3 ó x < -1 También se puede dar la respuesta en forma de intervalo

S = ]-∞, -1[ U ] 3,+∞[

Ejercicios propuestos

Halla la solución de las siguientes inecuaciones cuadráticas y representarla en la recta numérica.

• 6x2 + 7x ≤ 3
• x2 – 2x – 80
• x2 + 5x - 6 ≥ 0
• x2 – 7x ≤ -6

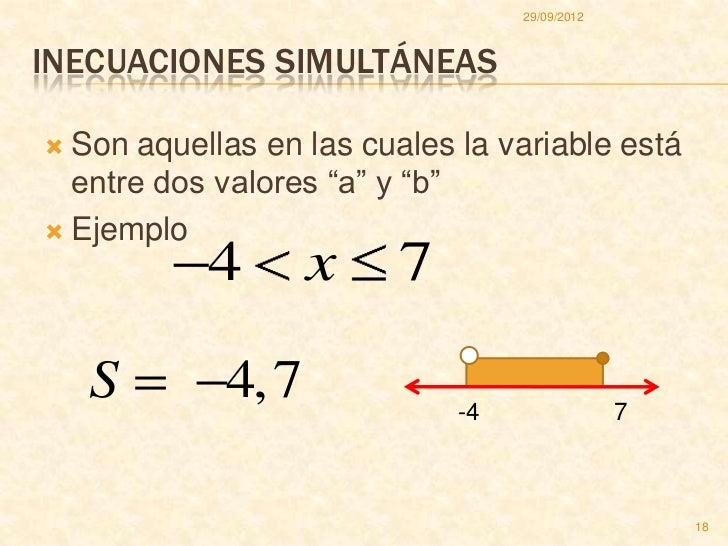
INECUACCIONES SIMULTANEAS

necuaciones simultáneas son las que se cumplen con el mismo valor o valores de la variable.

Ejemplo:

12.19 ¿Qué valores enteros verifican a la vez las dos desigualdades:

  ?

Respuesta: 19

Solución:

1º) Despejo la incógnita en ambas inecuaciones:

De momento conozco que el valor de la variable es menor que 20.

Calculo el valor de x en la segunda inecuación:

Ahora se que el valor de x es mayor de 18.

2º) Cuando una respuesta lleva el signo > y la otra, el signo < el valor de la variable ha de encontrarse en medio de ambas desigualdades:

 

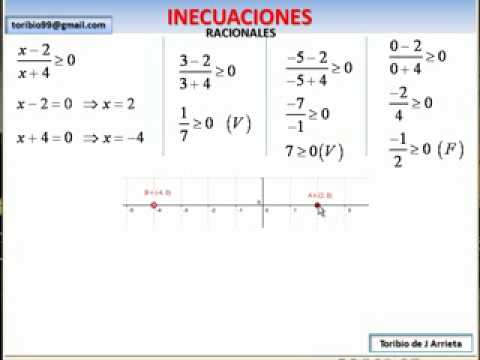
INECUACIONES RACIONALES

Son inecuaciones racionales, aquellas en las que tanto el numerador como el denominador son inecuaciones polinómicas cuadráticas o polinómicas de grado mayor a 2Es uno de los que trae más complicaciones, porque una inecuación racional es una expresión de tipo fracción, donde la variable está en el numerador y el denominador.

No olvide de:

1. No multiplicar en cruz
2. Para saber si el intervalo es abierto y cerrado
• El denominador siempre es abierto
• Numerador depende de la desigualdad

VALOR ABSOLUUTO

En matemáticas, el valor absoluto o módulo¹​ de un número real es su valor numérico sin tener en cuenta su signo, sea este positivo (+) o negativo (-).²​ Así, por ejemplo, 3 es el valor absoluto de +3 y de -3.

El valor absoluto está relacionado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos. El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como son los cuaterniones, anillos ordenados, cuerpos o espacios vectoriales.

Definición[editar]

El valor absoluto se define en cualquiera de los sistemas numéricos, de los números enteros, racionales, reales como:

• |a| = a si a ≥ 0;

• |a| = -a en otro caso; para un elemento a de los sistemas numéricos indicados.³​

Definiciones equivalentes[editar]

Si ${\displaystyle a}$ es un número real, su valor absoluto es un número real no negativo definido de las dos siguientes maneras:

1. ${\displaystyle |a|={\sqrt {a^{2}}}}$
2. ${\displaystyle |a|}$ es igual al máximo de {a, -a}.⁴